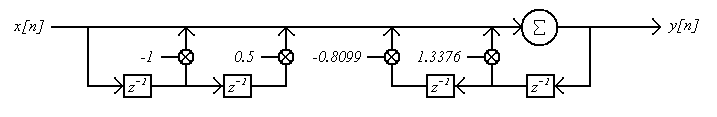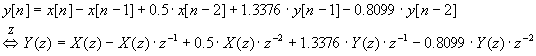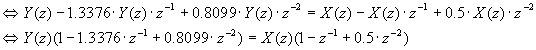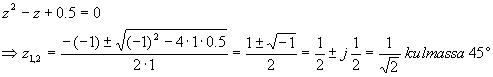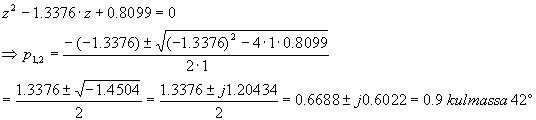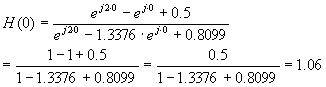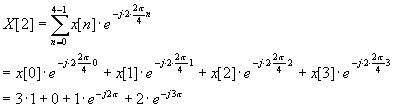|
|
|
|
|
|
Maksimipistemäärä on 6+10+6 =
22 pistettä. Läpipääsyyn riittää 8 pistettä.
Vastaa kaikkiin tehtäviin! |
|
|
|
|
|
|
1 |
Mitä tarkoittavat seuraavat termit ja lyhenteet?
Kirjoita lyhyt kuvaus termin tai lyhenteen tarkoittamasta asiasta! Kerro,
mikä on olennaista, ja mikä erottaa juuri tuon termin muista
samantapaisista asioista! |
|
|
|
|
|
|
|
|
1.2
|
systeemin stabiilius (2 p) |
|
systeemi on stabiili, jos sen vaste palaa vähintään asymptoottisesti
nollaan äärellisen syötteen jälkeen (1½ p)
systeemi on stabiili, jos sen navat sijaitsevat yksikköympyrän
sisällä (½ p)
FIR-systeemi on aina stabiili, IIR-systeemi vaatii stabiiliustarkastelun
(½ p)
|
|
|
|
|
|
1.3
|
impulssivaste (2 p) |
|
systeemin impulssivaste on se jono, jonka systeemi tuottaa yksikköimpulssijonosta
(1½ p)
merkinnät: yksikköimpulssijono d
[n] ja impulssivaste h[n] (½ p)
|
|
|
|
|
|
|
|
2 |
Systeemin differenssiyhtälö on |
|
|
|
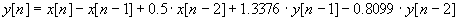
|
|
|
|
|
|
|
|
|
2.1
|
Piirrä systeemiä kuvaava lohkokaavio
(järjestelmäkaavio)! (2 p) |
|
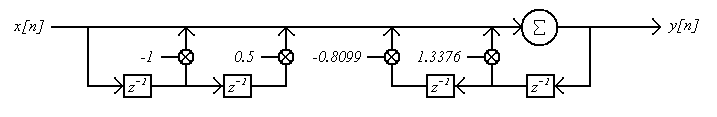 |
|
lohkokaavion voi piirtää hyvin monella tavalla
|
|
|
|
|
|
|
|
|
| 2.3 |
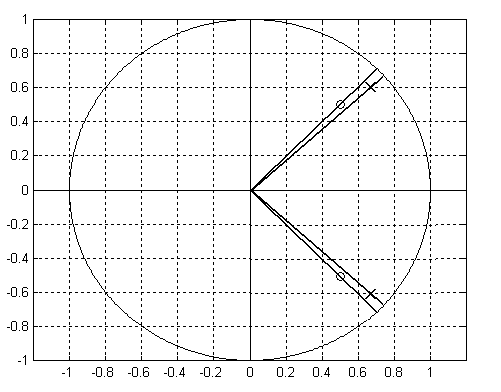
Määritä systeemin nollat ja navat
sekä piirrä ne yksikköympyrän kanssa kompleksitasoon!
(2 p) |
|
-
systeemin nollat saadaan siirtofunktion osoittajapolynomin nollakohdista,
navat nimittäjäpolynomin nollakohdista
-
nollat:
|
|
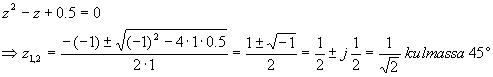
|
|
|
|
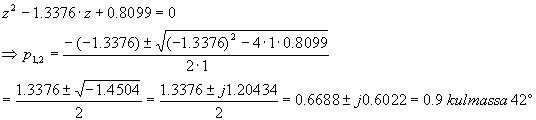
|
|
|
|
|
|
|
|
|
| 2.4 |
Laske systeemin vahvistus (amplitudivaste) taajuuksilla
0 ja p.
(2 p) |
|
-
sijoitetaan siirtofunktioon z:n paikalle ejw:
|
|
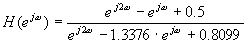
|
|
-
vahvistus taajuudella 0 saadaan sijoittamalla kulmataajuudeksi w
0 rad/s:
|
|
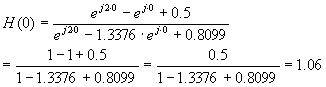
|
|
-
vastaavasti taajuudella p :
|
|
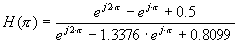
|
|
-
ej2pvastaa vektoria, jonka pituus
on 1 ja suunta 360° eli reaaliakselilla
plusykköseen yltävää vektoria. ejptaasen
vastaa vektoria, jonka pituus on myös 1, mutta suunta 180°
eli reaaliakselilla miinusykköseen yltävää vektoria,
joten
|
|
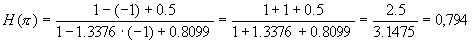
|
|
|
|
|
| 2.5 |
Hahmota systeemin amplitudivaste nolla-napa-kuviosta
päättelemällä! (2 p) |
|
-
amplitudivasteen hahmottamisessa käytetään hyväksi
nolla-napakuviota sekä edellä laskettuja vahvistusten arvoja.
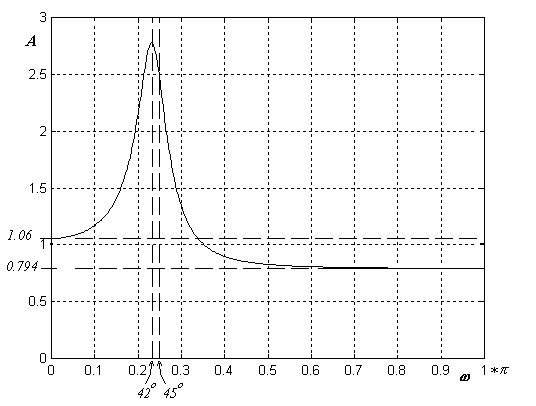
Amplitudivastekäyrä lähtee nollataajuudelta vahvistuksen
tasolta 1.06, nousee sieltä navan kohdalla maksimiarvoonsa (jonka
vahvistusta ei tarvinnut laskea) ja laskee nollan vaikutuksesta
taajuuteen p mennessä arvoon 0.794
|
|
|
|
|
|
|
|
|
|
3 |
Diskreetistä signaalista on valittu analysoitavaksi
neljän näytteen pituinen jakso |
|
|
|
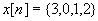
|
|
|
|
|
3.1
|
Laske jaksosta DFT-muunnos, kun k=2. (4 p) |
|
|
|
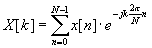
|
|
-
tässä tehtävässä näytejonon pituus on
neljä näytettä eli N=4, k=2
-
useassa ratkaisussa oli sekoitettu n ja x[n], vaikka kaava oli muistettu
täsmälleen oikeassa muodossa - soveltaessa olikin sijoitettu
järjestysnumero n arvon x[n] paikalle ja päinvastoin L
-
sijoitetaan tehtäväkohtaiset arvot kaavaan ja ratkaistaan
DFT:n arvo:
|
|
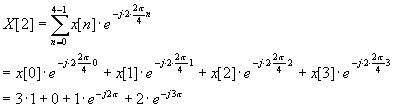
|
|
-
e-j2pvastaa vektoria, jonka pituus
on 1 ja suunta -360° eli reaaliakselilla
plusykköseen yltävää vektoria. e-j3ptaasen
vastaa vektoria, jonka pituus on myös 1 mutta suunta kolme piitä
eli kolme puolikierrosta vastapäivään - kyseessä on
siis miinusykköseen yltävä vektori , joten
|
|
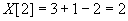
|
|
|
|
|
| 3.2 |
Mitä ylipäätään saadaan
selville DFT-muunnoksella? Mitä tehtävässä 3.1 laskemasi
DFT-muunnoksen tulos tarkoittaa? (2 p) |
|
-
DFT kertoo signaalin sisältämien taajuuskomponenttien suhteelliset
amplitudit sekä vaihekulmat. Taajuuskomponentteja saadaan selville
yhtä monta kuin on näytepisteitä. Näiden komponenttien
taajuudet jakaantuvat tasaisesti taajuusakselille välille 0ģ2p
eli tasasignaalista näytteenottotaajuuteen. k:n arvo nolla vastaa
tasasignaalia, arvo 1 vastaa taajuutta, jonka jakso on koko DFT:n kohteena
olevan näytejonon pituus sekunneissa. Tätä taajuutta voidaan
kutsua kyseisen näytejonon perustaajuudeksi. Jos näytejono on
esimerkiksi 20 ms pitkä ja näytteitä on näytejonossa
viisi kappaletta, on näytejonon pituus 5 x 20 ms = 100 ms. Tällöin
k=1 vastaa taajuutta, jonka jakso on 100 ms, eli taajuus on 1/100 ms =
1/0.1 s = 10 Hz. k:n arvo 2 vastaa edellistä taajuutta kaksinkertaisena
(esimerkissä siis 20 Hz), k:n arvo 3 taajuutta 30 Hz, jne
-
suhteelliset amplitudit saataisiin muutettua absoluuttisiksi jakamalla
ne näytejonon pisteiden lukumäärällä eli tässä
tehtävässä neljällä
-
tehtävässä 3.1 saatu tulos X[2]=2 tarkoittaa, että
näytejonossa on perustaajuuteen nähden kaksinkertaista taajuutta
kahden yksikön verran. Tämän taajuuskomponentin vaihekulma
on 0 eli taajuutta vastaava sinisignaali alkaa näytejonon kanssa samasta
kohdasta
|
|
|
|
|
|
|